Jeff Gore教授：生物种群中的合作、欺骗和崩溃行为

      4月8日晚，清华大学钱学森班"X-idea ——交叉创新挑战性问题"系列课程第十二讲在法图开讲。来自MIT的Jeff Gore教授受邀线上为同学们带来“生物种群中的合作、欺骗和崩溃行为”的物理生物学报告。报告采用线上线下同步直播的形式进行，吸引了百余名师生热情参与。本次课程由钱班2013级毕业生、MIT在读博士胡脊梁学长和钱班力8的朱笑寒同学联合主持。

      报告开始前，胡脊梁学长为大家带来了课程导读。他首先简要介绍了物理学和生物学交叉发展的概况。定量化革命对于物理学的发展十分重要，带来了学科规律的普适化和规模化应用。例如由托勒密唯象模型到第谷发展精准定量测量工具，再到最后牛顿统一经典力学规律，促成了科学和工程学的极大发展，出现了从赵州桥到跨江大桥的进步。生命科学目前仍处于唯象模型阶段，正处于定量革命的阶段，而物理模型在其中的应用将起到推动作用。之后，胡脊梁学长从微观尺度到宏观尺度列举了用光镊研究DNA力学特性、细胞分化背后的动力系统不同稳态、生物个体层面飞行速度-重量对应以及种群动力学等例子，展示了物理学、力学在生命科学中应用的巨大前景。

      随后，Jeff Gore教授在波士顿家中线上为同学们介绍了他的课题组对复杂生命系统的研究。他由湖泊生态系统污染后的稳态变化讲起，类比了生态系统和动力系统中许多特征的相似性。在这些系统中，各种组成成分的行为也具有明显的规律性，例如鱼群的协同防御行为和捕食者的协同捕猎行为。Gore教授课题组的主要方向便是在种群崩溃、演化等背景下，找到这些定量规律。

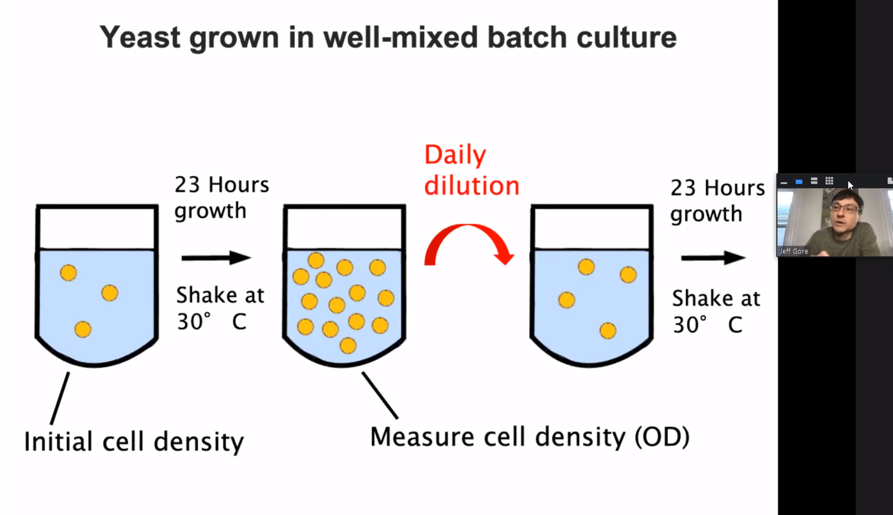
      Gore教授的课题组利用酵母开发了第一个可操作的实验室模型来验证理论预测的种群稳态和崩溃现象。在需要个体间协同利用外界资源时，酵母种群表现出在特定种群密度的迅速灭绝以及双稳态现象，这些现象可以被动力系统相关理论很好地预测。此外，种群中合作者、欺诈者的演化动态性也能被很好地量化。二者比例随种群数量变化在靠近临界点的曲线螺旋度增加现象也能够被理论正确预测。最后，Gore教授与大家讨论了种群的稳态转化问题。其中，不成功的入侵者能够通过改变环境间接改变种群稳态预测也得到了入侵细菌对重塑肠道菌群效果的验证。

      Gore教授的报告后，同学们针对挑战性问题进行了激烈讨论，提出了诸多创造性的想法。

一个物种种群内的协同行为如何演变？

      一组同学提出了两种可能的欺诈者和合作者的演化思路。欺诈者可能先于合作者产生：其合理性在于欺诈者所需的基因构成可能更为简单，而环境中又有足够的资源可以被该物种的每个个体独立利用。此后随着易利用资源的耗竭才出现合作者，并且这时合作者将因为能够利用复杂资源而获得生存优势。合作者也可能先于欺诈者产生：其合理性在于欺诈者所利用的简单资源可能由合作者产生，此时欺诈者相当于异养生物。

      另一组同学则试图为欺诈者和合作者共存的合理性提供解释。他们认为在“自私的基因”的背景下，合作者可能通过易化欺诈者的生存繁衍而增加自己的广义适合度，因为欺诈者携带大量合作者的基因。同时，有同学指出，这两种表型的比例可能随资源多少而变化，其中一定比例的欺诈者对资源更高效的利用可能会增加整个种群平均的适合度，从而使种群延续发展。

      另外，有同学在讨论时对发杂系统出现的机制提出了疑问。究竟是进化过程中自然会选择一些复杂系统相比独特的特征，还是越来越多的基因被保留下来以后，复杂系统自然地涌现出来？这个问题也得到了MIT在读博士生的高度认同。

种群数量在“临界点”附近如何随时间变化？

      一组同学提出，在真实情况中，种群往往不像实验室中酵母可控，因此，如何通过能够测量的有限种群的时空动态性来预测该物种的“临界点”将是很重要的问题。另外，如果能够预测这种“临界点”，我们便可以对有害种群进行更有效的杀灭。

      另一组同学则将Gore教授在动物种群中得出的结论应用到更广泛的场景。例如可以通过种群密度和临界点的参数估计多物种生境的交界处何种生物会占据优势；以及可以综合Gore教授课题组发现的时间上和空间上种群在“临界点”附近的动态规律来建立一个时空相互关联的方程，从而更好地模拟真实情况中种群边缘的数量动态性。

      此外，有同学提出在更复杂的生物系统中，由于记忆、适应等行为，同样的环境扰动可能对种群带来不同影响，从而造成种群数目“临界点”随时间改变的情况。模拟这样的情况将是由酵母稀释模型过渡到真实情况的必经之路。

      最后，胡脊梁学长对本次活动进行了简短总结。他肯定了同学们讨论出很多想法，认为其中有不少值得研究。他也着重强调了数学语言在描述生命复杂系统过程中的重要性。他同时也提到，诸如跨层级复杂度涌现现象等生命独有的过程，至今还未在模拟中复现，因此物理生物学领域也值得做更多探索。